my blog

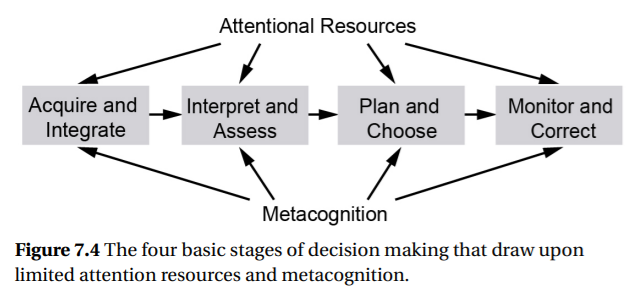
What is decision making? Generally, it is a task in which (a) a person must select one option from several alternatives, (b) a person must interpret information for the alternatives, (c) the timeframe is relatively long (longer than a second), (d) the choice includes uncertainty; that is, it is not necessarily clear which is the best alternative. By definition, decision making involves risk—there is a consequence to picking the wrong alternative—and so a good decision maker effectively assesses risks associated with each alternative. The decisions discussed in this chapter range from those involving a slow deliberative process, involving how to allocate resources to those which are quite rapid, with few alternatives, like the decision to speed up, or apply the brakes, when seeing a yellow traffic light, or whether to open a suspicious e-mail [362]. Decision making can generally be represented by four stages as depicted in Figure 7.4: (1) acquiring and integrating information relevant for the decision, (2) interpreting and assessing the meaning of this information, (3) planning and choosing the best course of action after considering the costs and values of different outcomes, and (4) monitoring and correcting the chosen course of action. People typically cycle through the four stages in a single decision.

Figure 7.4 The four basic stages of decision making that draw upon limited attention resources and metacognition.

1. Acquire and integrate a number of cues, or pieces of information, which are received from the environment and go into working memory. For example, an engineer trying to identify the problem in a manufacturing process might receive a number of cues, including unusual vibrations, particularly rapid tool wear, and strange noises. The cues must be selectively attended, interpreted and somehow integrated with respect to one another. The cues may also be incomplete, fuzzy, or erroneous; that is, they may be associated with some amount of uncertainty. 2. Interpret and assess cues and then use this interpretation to generate one or more situation assessments, diagnoses, or inferences as to what the cues mean. This is accomplished by retrieving information from long-term memory. For example, an engineer might hypothesize that the set of cues described previously is caused by a worn bearing. Situation assessment is supported by maintaining good situation awareness, a topic we discuss later in the chapter. The difference is that while maintaining SA refers to a continuous process, making a situation assessment involves a one time discrete action with the goal of supporting a particular decision. 3. Plan and choose one of alternative actions generated by retrieving possibilities from long-term memory. Depending on the time available, one or more of the alternatives are generated and considered. To choose an action, the decision maker might evaluate information such as possible outcomes of each action (where there may be multiple possible outcomes for each action), the likelihood of each outcome, and the negative and positive factors associated with each outcome. This can be formally done in the context of a decision matrix in which actions are crossed against the diagnosed possible states of the world that could occur, and which could have different consequences depending on the action selected. 4. Monitor and correct the effects of decisions. The monitoring process is a particularly critical part of decision making and can serve two general purposes. First, one can revise the current decision as needed. For example, if the outcomes of a decision to prescribe a particular treatment are not as expected, as was the case with Amy’s patient is getting worse, not better, then the treatment can be adjusted, halted or changed. Second, one can revise the general decision process if that process is found wanting and ineffective, as Amy also did. For example, if heuristics are producing errors, one can learn to abandon them in a particular situation and instead adopt the more analytical approach shown to the left of Figure 7.2. In this way, monitoring serves as an input for the troubleshooting element of macrocognition. Monitoring, of course, provides feedback on the decision process. Unfortunately, in decision making that feedback is often poor, degraded, delayed or non-existent, all features that undermine effective learning [11]. It is for this reason that consistent experience in decision making does not necessarily lead to improved performance [363, 357]. Figure 7.4 also depicts the two influences of attentional resources and metacognition. Many of the processes used to make ideal or “optimal” decisions impose intensive demands on perception and selective attention (for stage 1), particularly on the working memory used to entertain hypotheses in stage 2, and to evaluate outcomes in stage 4. If these resources are scarce, as in a multitasking environment, decision making can suffer. Furthermore, because humans are effort conserving, we often tend to adopt mental shortcuts or heuristics that can make decision making easier and faster, but may sacrifice its accuracy. Metacognition describes our monitoring of all of the processes by which we make decisions, and hence is closely related to stage 4. We use such processes for example to assess whether we are confident enough in a diagnosis (stage 2) to launch an action (stage 3) without seeking more information. We describe metacognition in more detail near the end of the chapter.7.3.1 Normative and Descriptive Decision Making Decision making has, for centuries, been studied in terms of how people should make optimal decisions: those likely to produce the best outcomes in the long run [364, 365]. This is called normative decision making. Within the last half century however, decision scientists have highlighted that humans often do not, in practice, adhere to such optimal norms for a variety of reasons, and so their decisions can be described in ways classified as descriptive decision making. We now discuss both the normative and descriptive frameworks. Normative decision making considers the four stages of decision making in terms of an idealized situation in which the correct decision can be made by calculating the mathematical optimal choice. This mathematical approach is often termed normative decision making. Normative decision making specifies what people should do; they do not necessarily describe how people actually perform decision-making tasks. Importantly, these normative models make many assumptions that incorrectly simplifies and limits their application to the decisions people actually face [366]. Normative models are important because they form the basis for many computer-based decision aids, and justify (often wrongly) that humans’ fallible judgment should be removed from the decision process [367]. Although such normative models often outperform people in situations where their assumptions hold, many real-life decision cannot be reduced to a simple formula [368]. Normative decision making revolves around the central concept of utility, the overall value of a choice, or how much eachoutcome is “worth” to the decision maker. This model has application in engineering decisions as well as decisions in personal life. Choosing between different corporate investments, materials for product, jobs, or even cars are all examples of choices that can be modeled using multiattribute utility theory. The decision matrix described in Chapter 2 is an example of how multiattribute utility theory can be used to guide engineering design decisions. Similarly, it has been used to resolve conflicting objectives, to guide environmental cleanup of contaminated sites [369], to support operators of flexible manufacturing systems [370], and even to select a marriage partner [371]. The number of potential options, the number of attributes or features that describe each option, and the challenge in comparing alternatives on very different dimensions make decisions complicated. Multiattribute utility theory addresses this complexity, using a utility function to translate the multidimensional space of attributes into a single dimension that reflects the overall utility or value of each option. In theory, this makes it possible to compare apples and oranges and pick the best one. Multiattribute utility theory assumes that the overall value of a decision option is the sum of the magnitude of each attribute multiplied by the utility of each attribute (Equation 7.1), where U(v) is the overall utility of an option, a(i) is the magnitude of the option on the i th attribute, u(i) is the utility (goodness or importance) of the i th attribute, and n is the number of attributes.

U(v) = به کتاب رجوع شود